Introduction
Separate Axis Theorem (SAT) is a method to determine whether two convex shapes are intersecting or not. The theorem states that, “Given two convex shapes there exists a line onto which their projections will be separate if and only if they are not intersecting”. It is the most commonly used method for collision detection. SAT also returns the minimum penetration vector, or minimum translation vector, the shortest distance that the colliding object can be moved in order to no longer be colliding.
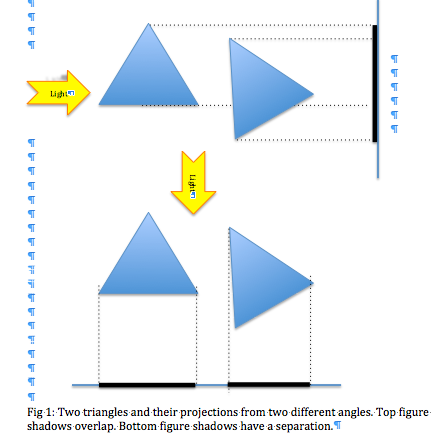
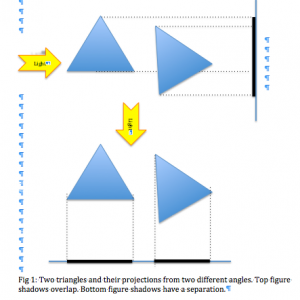
The basic idea is imagine you have two convex shapes, let us consider two triangles as given in fig 1. We shine light on them from different angles and observe shadows on the wall perpendicular to the direction of light, if doing this work around the shapes we do not find a gap in the shadows, then the objects are colliding. But, if we are able find a gap, then they are not intersecting/colliding.
Algorithm:
The first question that arises while implementing SAT which angles to test? The angles one should test are the normals of each shape edge. If one is given coordinates of the vertices then by simply flipping the coordinates and negating one can obtain the normal of the edge. This gives us the perpendicular vector to each edge of the shape, this is our testing axis and our virtual light is parallel to this axis. We determine all the possible testing axes for our shapes, for example for two triangles there will be six testing axes (three for each triangle), while for two squares we can have only four testing axes.
For each the testing axis is obtained, loop through every vertex of the first convex shape and project it onto the axis. Find the maximum and minimum values of all the projections. Repeat it for the second convex shape. Projection can be easily obtained from the dot product of the vertex in question and a normalized vector in the direction of testing axis.
To determine collision/intersection we need to compare the maximum projection of first convex shape with the minimum projection of the second shape. The distance between two should be greater than zero for no intersection. If for any of the testing axes we find a gap, then the two shapes are not intersecting.
In case one of the shapes is a circle then the axis (normal to circle) we need to test is the one that runs from the circle to the closest vertex of the second shape.
Pros and Cons
In case the two objects do not intersect one can exit from the loop after finding any axis that shows no overlapping. Thus it is fast and accurate.
SAT algorithm can be very computationally expensive in 3D and for complex polygons.