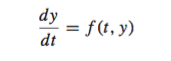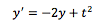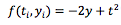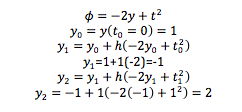A lot of problems in science and engineering involve solving differential equations pendulums, RLC circuits, diffusion and so on. An ordinary differential equation can be expressed as:
Generally solution of this equation is of the form:
Here ‘phi‘ is the increment function or slope and h is the step size. Thus, an estimate of slope is used to extrapolate the new value y(i+1) when the previous value y(i) is known, over a distance h. The methods which are based on above equation are called one step methods. They all only differ by the definition of increment function.
Solved Example:
Calculate y(2) for in the interval t=[0,2]. Given y(0)=1, for
Solution:
Consider h=1, here
Using Euler Method: