Finding the “Best” You (Well, the Best Model Anyway!)

Welcome back to All that is under the Sun, your friendly guide through the fascinating, and sometimes bewildering, world of Artificial Intelligence. This month, we’re kicking off a brand-new series that gets to the very heart of how AI learns and improves. Think of it as the AI equivalent of a motivational seminar, a Marie Kondo decluttering session, and a treasure hunt all rolled into one. We’re talking about Optimisation in Machine Learning: The Quest for the “Best” Model.

Ever wondered how Netflix just knows what you want to binge next? Or how your email magically filters out (most of) that spam? Or how those mind-blowing AI art generators conjure up images from a simple text prompt? The secret sauce, my friends, has a big dollop of optimisation in it.

Check the video version: YouTube

So, What’s This “Optimisation” Hullabaloo All About?

At its core, optimisation in machine learning is the process of finding the best possible set of parameters or settings for a machine learning model to achieve a specific goal. “Best” is the keyword here. But “best” can mean different things depending on the task.

• For a model predicting stock prices, “best” might mean the lowest prediction error.
• For a self-driving car, “best” involves a complex cocktail of safety, efficiency, and smoothness of the ride. (No one wants a jerky robot chauffeur, right? 🤢)
• For an AI image generator like DALL-E or Midjourney, “best” means creating an image that most accurately and artistically represents the given text prompt.

Think of it like trying to bake the perfect cake. You have a recipe (the model architecture), ingredients (the data), and various knobs you can tweak: the amount of sugar (a parameter), the oven temperature (another parameter), the baking time (yet another parameter). Optimisation is the process of experimenting with these knobs, maybe a little less sugar, a slightly cooler oven, a few more minutes of baking, until you get a cake that’s not just good, but perfectly moist, fluffy, and delicious. Your taste buds (or in ML, a specific metric) tell you how close you are.

In machine learning, our “knobs” are called parameters (often, a looooot of them, sometimes billions!). These are internal variables that the model uses to make predictions or decisions. For instance, in a simple linear regression model (predicting a value like house price based on size), the parameters are the slope and intercept of the line. For a complex neural network, these parameters are the “weights” and “biases” of its numerous interconnected “neurons.”

The goal of optimisation is to adjust these parameters iteratively so that the model performs its task as accurately or efficiently as possible. It’s about moving from a state of “meh, that’s an okay prediction” to “WOW, that’s spot on!“

Why Bother Optimising? Can’t We Just Get it Right the First Time?

Ah, if only life (and AI) were that simple! Imagine trying to hit a tiny bullseye on a dartboard, blindfolded, from 50 paces away, on your very first throw. That’s kind of what it’s like to initialise a machine learning model with random parameters. You’re unlikely to nail it.

Optimisation provides a systematic way to get closer and closer to that bullseye. Without it:

• Your AI would be pretty dumb: Imagine a spam filter that lets all the Nigerian prince emails through but flags your grandma’s cookie recipes. Not ideal.
• Predictions would be wildly inaccurate: A medical diagnosis AI that’s only 30% accurate? No, thank you!
• Resources would be wasted: Inefficient models can take longer to train and run, costing more in terms of time and computational power (think $$$ for those fancy GPUs).

Real-world AI showpieces are monuments to successful optimisation.

• AlphaFold (DeepMind): This revolutionary AI predicts protein structures with incredible accuracy. Finding the right “fold” for a protein is an incredibly complex optimisation problem. AlphaFold’s success comes from its sophisticated architecture and its ability to optimise its parameters to understand the subtle rules governing protein folding. This has massive implications for drug discovery and understanding diseases.
• Tesla’s Autopilot: While still evolving, the ability of a Tesla to navigate roads, identify obstacles, and make driving decisions relies heavily on optimising complex neural networks. These networks are trained on vast amounts of driving data, and optimisation algorithms continuously fine-tune them to minimise driving errors and maximise safety and smoothness. Every software update likely includes improvements gleaned from further optimisation.
• Recommendation Systems (Netflix, Spotify, Amazon): That uncanny feeling when a platform suggests something you actually love? That’s optimisation at work! These systems optimise their algorithms to maximise user engagement (clicks, views, purchases) by fine-tuning how they weigh different factors (your viewing history, what similar users like, item popularity, etc.).

Optimisation is the engine that drives learning in AI. It’s the process by which a model learns from data.

The “How-To” of Optimisation: A Sneak Peek (No Math Overload, Promise!)

So, how does this magical “knob-tweaking” happen? While there are many sophisticated algorithms, the fundamental idea often revolves around something called a loss function and an optimiser.

1. The Loss Function (The “Ouch!” Meter): First, we need a way to tell the model how badly it’s doing. This is where the loss function (or cost function or error function) comes in. It quantifies the difference between the model’s prediction and the actual “ground truth” value.
   • If our model predicts a house price is $300,000, but it actually sold for $350,000, the loss function would spit out a number representing that $50,000 error.
   • A high loss value means “Ouch! You’re way off!” A low loss value means “Not bad, getting warmer!” The goal of optimisation is to minimise this loss.
2. The Optimiser (The “Smart Knobtweaker”): This is the algorithm that actually adjusts the model’s parameters to reduce the loss. The most famous family of optimisers is based on Gradient Descent. Imagine you’re on a foggy mountain (the “loss landscape”) and you want to get to the lowest valley (minimum loss). You can’t see the whole map, but you can feel the slope of the ground beneath your feet. Gradient Descent says: “Take a step in the steepest downhill direction.” You repeat this process, step by step, and hopefully, you’ll eventually reach the bottom. The “gradient” is just a bit of calculus magic that tells us the direction of the steepest ascent. So, we go in the opposite direction (steepest descent). The “learning rate” is a hyperparameter (a knob we set before training) that determines how big those steps are. Too big, and you might overshoot the valley. Too small, and it’ll take forever to get there (like watching paint dry, but with more math). We’ll dive much deeper into loss functions (like Mean Squared Error for predicting numbers, and Binary Cross-Entropy for yes/no predictions) and Gradient Descent in our upcoming posts. Get ready for some cool visualisations!

A Tiny Taste of Code: Watching Our AI Baby Learn to Walk (Well, Calculate!)

Alright, theory is great, but let’s get our hands slightly dirty with a conceptual code snippet. We won’t build a full-blown neural network here (we’ll save some fun for later!), but we can illustrate that magical “getting better” process with a super simple model.

Imagine our model is trying to solve a basic equation: target_value = parameter * input_data. If input_data is 4 and the target_value is 20, our AI’s grand mission is to figure out that the parameter should be 5. Simple for us, a learning journey for our code!

We’ll start with a guess for our parameter (say, 2 – clearly not right!) and iteratively nudge it closer to the true value using a learning_rate and the error in its prediction.

Here’s a peek at the core idea (you’ll find the full interactive code with all the bells and whistles, including the plotting magic, in a Jupyter Notebook linked at the end!):

# Essential setup
input_data = 4
target_value = 20
parameter = 2.0  # Our initial (wrong) guess, using a float
learning_rate = 0.1 # How big of a step to take

# Lists to store our learning journey
iterations_log = []
predictions_log = []
errors_log = []
parameters_log = []

# The "learning" loop
for i in range(100): # Let's give it up to 100 tries
    # 1. Make a prediction
    prediction = parameter * input_data
    
    # 2. Calculate the "ouch!" (error)
    error = target_value - prediction
    
    # 3. The "nudge": Adjust the parameter
    # This simple rule says: if error is positive (prediction too low), 
    # increase parameter. If negative (prediction too high), decrease it.
    # The 'input_data' scales the adjustment appropriately.
    parameter_update = error * input_data * learning_rate
    parameter = parameter + parameter_update
    
    # Log our progress
    iterations_log.append(i + 1)
    predictions_log.append(prediction)
    errors_log.append(error)
    parameters_log.append(parameter)
    
    # Stop if we're close enough (no need to overdo it!)
    if abs(error) < 0.001:
        print(f"Converged early at iteration {i+1}!")
        break

# (The full code also includes matplotlib magic to generate the plots below)

What’s happening here?

Our little code snippet is like a diligent student. In each iteration:

1. It makes a prediction using its current parameter.
2. It calculates the error: how far off is the prediction from the target_value?
3. It then updates the parameter in a direction that it “thinks” will reduce the error next time. The learning_rate prevents it from making too drastic a change (like a student who overcorrects wildly after one mistake).

Visualizing the “Aha!” Moments

And this is where it gets really cool! If we plot how our prediction, error, and parameter change over the iterations, we can see the learning process. (Imagine these plots appearing right here in the blog post – you’ll generate them from the notebook!)

(Here, you would embed the actual plots you generate from your script. I will describe what each plot, based on your code, would show):

1. Prediction vs. Iteration: Check this out! Our blue “Prediction” line starts off way below the red dashed “Ground Truth (Target)” line of 20 – that’s our model making its initial, uninformed guess (predicting around 8, since our parameter started at 2). Then, whoa! It takes a confident leap and overshoots the target in the next iteration, going up to nearly 27! It’s like an overeager student. But then, it quickly realises its mistake, comes back down, maybe overcorrects a tiny bit again, and then elegantly settles in, oscillating less and less until it cosies up right to our target value of 20. That “settling down” is the optimisation kicking in!
2. Error vs. Iteration: This orange line is our “Ouch Meter,” and it tells a similar story. The error starts big and positive (around 12, because 20 minus ~8 is ~12). When the prediction overshot, the error swung to become negative (around -7). You can see it bounce back and forth across the zero line, with each bounce getting smaller. This dance around the zero-error line, gradually calming down, is exactly what we want to see – our model is learning to reduce its mistakes with each step until the error is practically non-existent. Zero error = happy model!
3. Parameter vs. Iteration: This green line is the star of our show – the parameter we’re trying to optimise! We wanted it to reach the “True Parameter” value of 5 (the red dashed line). It looks like after the first update (based on the initial guess of 2, not shown pre-update on this iteration axis), it jumped way up to almost 6.8! Again, a bit too enthusiastic. Then it undershot, dropping to around 4. But like a determined little trooper, it oscillates – overshooting, then undershooting – with each correction getting more precise, until it locks onto that magic number 5. This is the actual “knob” inside our model being tuned perfectly.

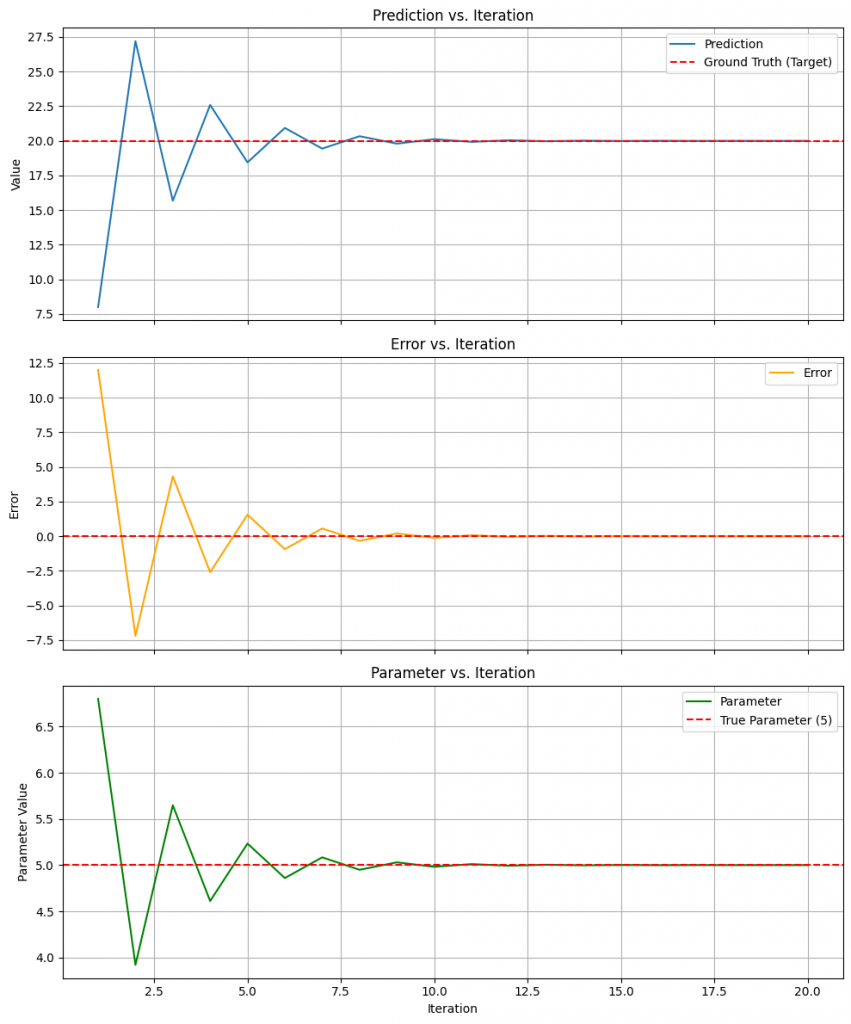
Isn’t that neat? That slight wobble and then homing in on the target is so characteristic of these iterative processes. It’s not always a perfectly smooth ride to the “best” answer, but a series of adjustments and corrections. This little dance of the lines – the overshooting, the dampening oscillations, the eventual convergence – is a fantastic visual for how optimization algorithms guide a model from cluelessness to (in this case, numerical) wisdom.

This iterative refinement, this journey from a wild guess to a precise answer, is the essence of optimisation in action. It’s not a one-shot deal but a patient, step-by-step process of getting better.

Here is GitHub link – copy the code on Colab and have fun!

Why This Matters to YOU (Even if You’re Not Building Skynet)

Understanding optimisation is crucial for anyone working with or interested in AI, for several reasons:

• For Professionals: If you’re a data scientist, ML engineer, or developer, optimisation is your bread and butter. Choosing the right optimisation algorithm, tuning its hyperparameters (like the learning rate), and diagnosing optimisation problems are key to building effective models. Understanding the trade-offs between different optimisers (e.g., Adam, SGD, RMSprop) can make a huge difference in training time and model performance. Knowing how parameters are “learned” helps you debug and improve your creations.
• For the General Public & Business Leaders: Knowing that AI models “learn” by being “optimised” helps demystify AI. It’s not magic; it’s a sophisticated process of trial and error guided by mathematics. This understanding helps in appreciating AI’s capabilities and limitations. When a company says their “AI is constantly improving,” it often means they are continuously collecting new data and re-optimising their models. It also helps you ask better questions: How is this AI model optimised? What data is it learning from? What biases might be in that data that could lead to a sub-optimal or unfair “best” model?

Optimisation ensures that the AI tools we use are becoming more accurate, more efficient, and ultimately, more useful. It’s the difference between a clumsy robot and a graceful one, a clueless chatbot and a helpful virtual assistant.

---

The Road Ahead: More Optimisation Goodness!

Phew! That was a whirlwind tour of the “what” and “why” of optimisation. But we’ve only just scratched the surface. In the future posts, we’ll be rolling up our sleeves and diving into:

1. Loss Functions: Quantifying Error (How do we tell the AI it’s wrong, and by how much?)
2. Loss Function: Mean Squared Error (MSE) (The workhorse for regression problems)
3. Loss Function: Binary Cross-Entropy (The go-to for telling cats from dogs, or spam from not-spam)
4. The Concept of Gradient Descent (The granddaddy of optimisation algorithms – how we iteratively minimise that loss)
5. Visualising Gradient Descent (Let’s actually see that “walking down a hill” magic!)

By the end of this series, you’ll have a solid grasp of how machine learning models go from clueless to clever.

Got questions? Burning thoughts? Or perhaps a brilliant cake analogy for optimisation I missed? Hit reply or drop a comment! We love hearing from you.

And if you found this helpful, why not share the blog with a friend or colleague who’s curious about the AI revolution?

Until next time, keep learning, keep questioning, and may your models always converge to the global minimum! 😉

Stay tuned & stay simplified!